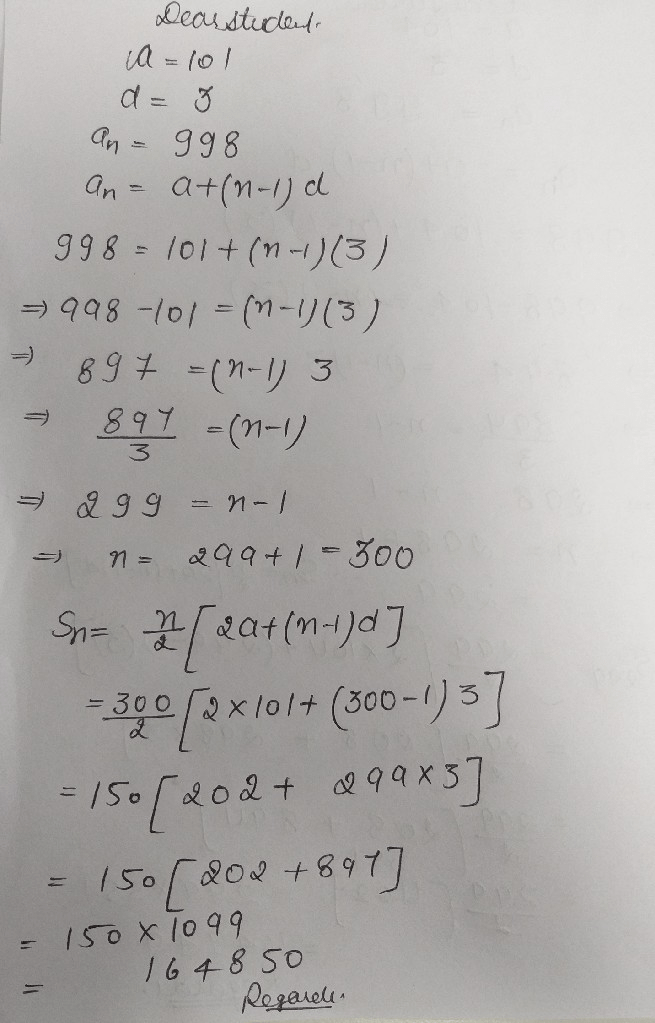What Is The Sum Of All 3 Digit Numbers. Each possible three digit number is a linear combination of digits. 5q+3 starting with q=20 we get 3 digitsnumbers 103,108,113,…….

Sum of all three digit numbers formed using 1 3 4 (without repetition) list of numbers formed using the digits 1, 3, 4 since we are going to form three digit numbers, let us have three blanks. Each possible three digit number is a linear combination of digits. So in the second grid the tens units sum to 4 ⋅ 81 ⋅ 10 = 3240.
 Source: brainly.in
Source: brainly.in
____ ____ ____ the first blank (hundred's place) has three options from the given three digits. Each possible three digit number is a linear combination of digits.
If The New Number Formed By Reversing The Digits Is Greater Than The Original Number By 18.
For example, adding 1, 2, 3, and 4 gives the sum 10, written. No of 1 s depends on number of digits. In total we have 18 such numbers so, s 18= 218(2×13+17×5)=999 was this answer helpful?
53 ⋅ 555 = 125 ⋅ 555 = 69375 Answer Link
N 2 ( first term + last term), n is the number of total terms in the series. Therefore, by applying the above formula the sum of all 3 digit numbers will be: We got 20 as follows.
Can Only Occur For 2 Times In Units/Tens/Hundreds Place.
If we have 0 in units place we can form a number in 4*5 ways. The sum of all 3 digit numbers that can be formed from the digits 1 to 9 and when the middle digit is a perfect square is (repetitions are allowed). = (112/2) (104 + 992) = 56 x 1096 = 61376 so, the sum of all 3 digit numbers divisible by 8 is 61376.
Check If All Bits Can Be Made Same By Single Flip.
How do you find the sum of 4 numbers? In the third grid the tens units sum to 9 ⋅ 81 ⋅ 10 = 7290 then to find the total we add up all the hundreds: We have ( 999 − 100) + 1 = 900 terms in our series.
They Are 1, 3, 4
In mathematics, summation is the addition of a sequence of any kind of numbers, called addends or summands; + 23) = 42 (26*21/2) = 11466. If we add up all the numbers we will get